Ah The Joy of Maths!
In my research, one of the criteria for the patients I recruit is that their Body Mass Index (BMI) must be more than 28. Body Mass Index is an indicator for one's weight status while considered together with their height. It's calculated with the following formula:
As my daily routine, I go through all the surgery patients' history, have a look at the doctor's notes, and find out whether they fulfill this BMI criteria. Sometimes it's quite easy, as in some of the notes all the height, weight and even the BMI value itself are already recorded. But in some other notes, the only things I could find are the height and the weight, or sometimes weight alone. That makes it hard for me to work out whether they are suitable for my study, and if it's not a clearly very-heavy or very-light weight, I would then have to take out my handphone to calculate the BMI.
But all that is time consuming, and I was a bit frustrated. I thought that there ought to be some better ways of doing the calculation.
 Today, while playing around with a BMI calculator (pictured on the right), I noticed an interesting pattern. After some twiddling and calculation, I figured out that if I take one's height in centimetre, subtract it by about 90, I would get the approximate weight of the person if their BMI is 28!
Today, while playing around with a BMI calculator (pictured on the right), I noticed an interesting pattern. After some twiddling and calculation, I figured out that if I take one's height in centimetre, subtract it by about 90, I would get the approximate weight of the person if their BMI is 28!For example, let's say you are 1.73m tall. I would just subtract 90 from 173, and hence 83 kilo would be your weight if your BMI is 28! So now keeping that in mind, if I see that you are 88 kilo, I would be glad that you are good for my study.
By checking my results against calculator and the BMI calculator, I found that there is still quite a bit of discrepancy between my approximation and the actual result. So I plotted out the two following equations
- y = 28x2
- y = 100x-90
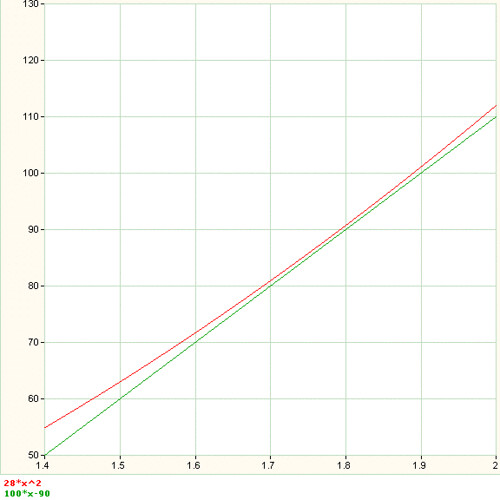
As you can see here, the red line is the actual weight which corresponds to BMI of 28; while the green line is the approximation I got using my "subtract 90" formula. While the green line gives a good approximation for common heights (1.5m to 1.9m); you can see that there is still a little gap between the two graphs, and I thought, why not make it even better? I found that if I subtract 89 instead of 90 from the cm, this is the graph that I would get:
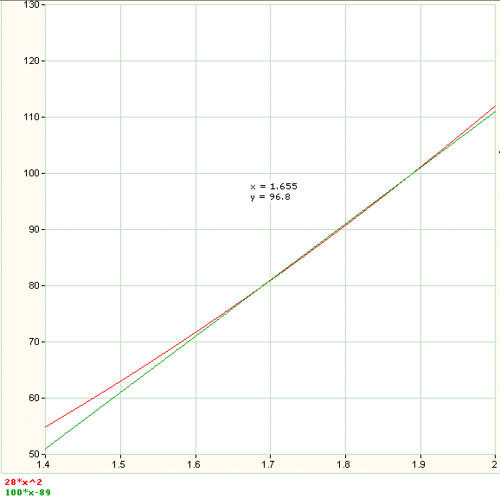
Much better! For 1.65m to 1.90m, there's almost a perfect overlap between the two graphs; while for 1.50m to 1.65m, the discrepancy is only 1 to 2kg. I am happy with the result!
But here comes the problem. With this formula, you have to take 89 from the person's height in cm, and subtracting 89 isn't that intuitive to do. But then, I figured that if you take away the first digit and add 11 to it, it would be the same as subtracting 89.
So here is my complete solution.
- Get the person's height in cm.
- Ignore the 1 at the front, add 11 to the cm. (e.g. if one's height is 170cm, make it 70 + 11 = 81)
- If the patient is heavier than this, he's heavy enough for my study! :)
- Get the person's weight in kg.
- Take away 11 from the weight, and add a 1 at the front. (e.g. if one's weight is 90kg, make it 90 - 11 = 79 ---> 179cm
- Then I would make an educated guess. If it is a female patient, then she would be likely to be shorter than 179, so she should be heavy enough for the study. If it's a male patient, there's a slight chance that he's tall enough to actually have a BMI of less than 28.
Note: By the way, this BMI calculator is a kind of special slide rule, my favourite mathematical gadget!
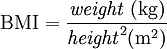







3 comments:
This post sounds a little bit geeky to me. haha
Another thing is I am kinda looking forwards to you Abused Probability 3.
It indeed IS geeky. :P
Yeah I will write the part 4 of Abused probability when I have the mood to. Haha sorry oh. I am a slacker, and I only write blog posts (especially the long ones) when I am slacking very badly. :P
Post a Comment